Объем воды в СО. Формулы расчетов

Объем воды в СО. Формулы расчетов

Самый простой способ рассчитать объем трубы – воспользоваться онлайн сервисом или специальной десктопной (настольной) программой. Второй способ – вручную, и для этого понадобится обычный калькулятор, линейка и штангенциркуль, которым измеряют внутренний и наружный радиусы трубы (на всех чертежах и схемах радиус обозначается символом R или r). Можно воспользоваться значением диаметра (D или d), который вычисляется по простой формуле: R x 2 или R². Чтобы вычислить объем воды в трубе в кубах, также понадобится узнать длину цилиндра L (или l).

Измерение внутреннего радиуса позволит узнать, сколько воды или другой жидкости в цилиндре. Результат отражается в кубических метрах. Знать наружный диаметр трубы необходимо для расчета габаритов того места, где будет прокладываться трубопровод.

Последовательность расчетов такова: сначала узнаю́т площадь сечения трубы:

1. S = R x ∏;
2. Площадь цилиндра – S;
3. Радиус цилиндра – R;
4. ∏ – 3,14159265.

Результат S умножают на длину L трубы – это и будет полный рассчитанный объем. Расчет объема по сечению и длине цилиндра выглядит так:

1. V_тр = S_тр x L_тр;
2. Объем цилиндра – V_тр;
3. Площадь цилиндра – S_тр;
4. Длина цилиндра – L_тр.

Пример:

1. Стальная труба Ø = 0,5 м, L = 2 м;
2. S_тр = (D_тр / 2) = ∏ х (0,5 / 2) = 0,0625 м².

Конечная формула, как рассчитать объем трубы, будет выглядеть следующим образом:

V = H х S = 2 х 0,0625 = 0,125 м³;

Где:

H – толщина стенки трубы.

Толщина стенок любой трубы

Эта формула позволяет узнать, как посчитать объем трубы с любыми заданными параметрами и из любого материала, а также отдельные участки составного трубопровода. Чтобы не путаться в параметрах результатов, необходимо сразу выражать их в одних и тех же единицах, например, в метрах и кубических метрах, или в сантиметрах и кубических сантиметрах. Из компьютерных программ для начинающих пользователей или для тех, кто предполагает проводить одноразовые расчеты, можно предложить  VALTEC.PRG,  Unitconverter, Pipecalc и другие.

Объем воды в бассейне. Как рассчитать объем бассейна

Что это такое, когда его необходимо высчитывать?

Объем — это произведение площади основания на высоту. Если речь идет о бассейнах, необходимо различать два показателя — вместимость чаши и количество воды в ней. Первое число всегда больше, так как воду никогда не наливают вровень с бортиками.

Количество воды надо знать в следующих случаях:

1. Подсчет концентрации химических препаратов.
2. Расчет производительности циркуляционной системы и фильтров.
3. Определение расхода при подаче или сливе воды из чаши.
4. Определение веса и величины давления на фундамент.

Второе значение — вместимость ванны — требуется при подсчетах:

• количество строительных и отделочных материалов;
• высота лестницы;
• определение мощности аттракционов (высота волны или силы противотока).

Кроме этого, знание емкости ванны требуется при расчете производительности инженерных систем — вентиляции, освещения, кондиционирования и т.п.

Как рассчитать объём бассейна самостоятельно?

Объём чаши — это количественная характеристика пространства, занимаемого водой.

Прямоугольный

Формула для расчёта объёма воды в прямоугольной чаше: длина х ширина х средняя глубина = объём воды (куб. м).

Пример (размеры указаны в метрах):

• длина — 14;
• ширина — 6;
• средняя глубина — 1,5.

Пример расчёта: 14 х 6 х 1,5 = 126 куб. м

Бассейн прямоугольной формы:

Круглый

Формула расчёта объёма в круглой чаше: диаметр х диаметр х средняя глубина х 0,78 = объём воды (куб. м).

Пример (размеры указаны в метрах):

• диаметр круглого пула — 6;
• средняя глубина — 1,5.

Рассчитываем: 6 х 6 х 1,5 х 0,78 = 42,12 куб. м (округляем в большую сторону — 43 куб. м)

Овальный

Расчётная формула для объёма овальной чаши: длина х ширина х средняя глубина х 0,89 = объём воды (куб. м).

Пример (размеры указаны в метрах):

• длина — 12;
• максимальная ширина — 6;
• средняя глубина — 1,5.

Пример расчёта: 12 х 6 х 1,5 х 0,89 = 96,12 куб. м (округляем до 97 куб. м).

Бассейн овальной формы:

Выбор ширины

Показатель аргументируется двумя моментами:

• Эксплуатационный. Если будет плавать один человек достаточно ширины 2 м;
• Эстетическая составляющая. Здесь установлено стандартное правило. Все прямоугольные сооружения выпускаются в размере длина/2;
• Индивидуальные параметры доступны только в процессе приобретения конструкции, выполненной на заказ. Бассейны готового типа выпускаются в таких стандартных габаритах, как 3×2, 4×2, 5×2,5, 6×3, 7×3,5 м.

Детские искусственные водоемы — это переносные надувные модели. Они имеют круглую форму. Отличным вариантом для малышей считается диаметр 2-3 метра. Для подростков стоит приобретать прямоугольные конструкции относительно небольших размеров.

Калькулятор для расчёта

Имеются специализированный компьютерный сайт, помогающий в вычислении объёма бассейна (куб. м): https://водород-бассейн.рф/kalkulyator-rascheta-obyema-vody/

Первоначально надо иметь сведения о некоторых показателях:

• Запланированная глубина будущего бассейна. Если она во всех местах одинаковая — обходятся одним значением, если резервуар где-либо заглубляется — необходимо два значения: большее и меньшее, чтобы определить среднее значение глубины.
• Длина и ширина водоёма. Самые значимые параметры — от них зависит размер, пространство, занимаемое бассейном.

Объем воды в трубе диаметро. По какой формуле проводится расчет

Чтобы получить точные данные, необходимо приготовить:

• Калькулятор;
• Штангенциркуль;
• Линейку.

Сначала измеряется радиус, обозначенный буквой R. Он может быть:

• Внутренним;
• Наружным.

Первый позволяет высчитать, какое количество жидкости, способно поместиться в цилиндре, то есть внутренний объем трубы, ее кубатура.

Внешний радиус, необходим для определения размера места, которое она займет.

Для расчета необходимо знать данные диаметра трубы. Его обозначают буквой D и рассчитывают по формуле R x 2. Определяется также длина окружности. Обозначается буквой L.

Чтобы вычислить объем трубы, измеряемого кубическими метрами (м3), необходимо предварительно рассчитать ее площадь.

Для получения точного значения, требуется сначала рассчитать площадь сечения.
Для этого применяют формулу:

• S = R x Пи.
• Искомая площадь — S;
• Радиус трубы – R;
• Число Пи — 3,14159265.

Полученное значение нужно перемножить на длину трубопровода.

Как найти объем трубы по формуле? Нужно знать всего 2 значения. Сама формула расчета, имеет следующий вид:

• V = S x L
• Объем трубы – V;
• Площадь сечения – S;
• Длина – L

К примеру, у нас есть металлическая труба диаметром 0,5 метра и длиной два метра. Для проведения расчета в формулу расчета площади круга, вставляется размер внешней поперечины нержавеющего металла. Трубная площадь будет равна;

S= (D/2) =3,14 х (0,5/2) = 0,0625 кв. метра.

Итоговая формула расчета, примет следующий вид:

V = HS = 2 х 0,0625=0,125 куб. метра.

По этой формуле рассчитывается объём совершенно любой трубы. Причем абсолютно не важно из какого она материала. Если трубопровод имеет много составных частей, применяя эту формулу, можно рассчитать по отдельности, объем каждого участка.

При выполнении расчета, очень важно чтобы размеры выражались в одинаковых единицах измерения. Проще всего проводить расчет, если все значения перевести в квадратные сантиметры.

Если использовать разные единицы измерения, можно получить весьма сомнительные результаты. Они будут очень далеки от настоящих значений. При выполнении постоянных ежедневных вычислений, можно использовать память калькулятора, установив постоянное значение. К примеру, число Пи, умноженное на два. Это поможет намного быстрее произвести расчет объема трубы разного диаметра.

Сегодня для расчета можно использовать готовые компьютерные программы, в которых, заранее указываются стандартные параметры. Для выполнения расчета, нужно будет только вписывать дополнительные переменные значения.

Объем воды в трубе. Калькулятор для расчета объема трубы в литрах

Объем трубы в литрах можно рассчитать с помощью онлайн калькулятора двумя способами:

1. указав наружный диаметр в мм, длину трубы в метрах и толщину стенки в мм. Будет удобен для вычисления объема в литрах для тех труб, у которых указана толщина стенок в нанесенной на нее маркировке, например, полипропиленовые для пайки и/или для скрутки фитингом.
2. указав внутренний диаметр в мм и длину трубы в метрах (погонные метры).

Делая расчет объема трубы в литрах, необходимо помнить о возможных погрешностях, например, повороты, неполная заполняемость некоторых участков труб и т.д.

Рассчитать объем трубы в литрах, калькулятор

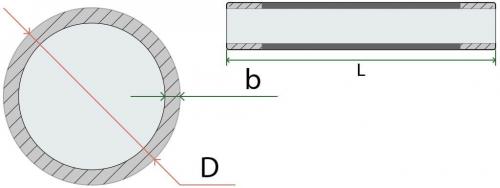
• Зная толщину стенки, диаметр и длину

• Зная диаметр и длину

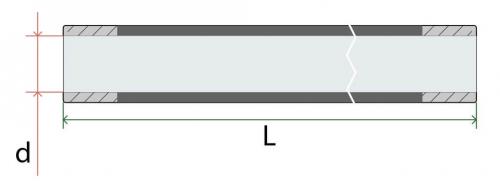
Как рассчитать объем трубы в литрах?

Чтобы узнать внутренний диаметр трубы, зная наружный, необходимо толщину стенки ( b ) умножить на 2, результат вычесть из наружного диаметра ( D ).

Формула выглядит следующим образом: Внутренний диаметр трубы = D - ( b * 2 )

Также можно воспользоваться таблицами, например, трубы для пайки. В которой уже указаны толщина стенки и ее диаметры для PN10, PN20 и PN25.

Для расчета объема цилиндра применяют формулу: V = Пи * R² * h = Пи * ( d² / 4 ) * h, где:

• Пи — 3,1415926;
• R – радиус цилиндра;
• d – диаметр цилиндра, в нашем случае — внутренний диаметр трубы;
• h – высота цилиндра, в случае расчета объема трубы h заменяем на L — длину трубы.

Исходя из этого, формула для расчета объема трубы по известному, внутреннему диаметру примет вид:

V объем трубы = Пи * ( d² / 4 ) * L

Важно! Перед началом расчета с помощью формул, все размеры необходимо перевести в единую меру, т.е. — сантиметры или дециметры.

Пример расчета объема трубы в литрах

D (наружный диаметр трубы) = 17 мм, b (толщина стенки) = 1,3 мм, L (длина трубы) = 10 м.

Объем воды в цилиндре. Объем жидкости в цилиндрической таре

Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.И это не праздности ради, а дела для.

Цитирую запрос пользователя:Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?

Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем :) Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.

Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.

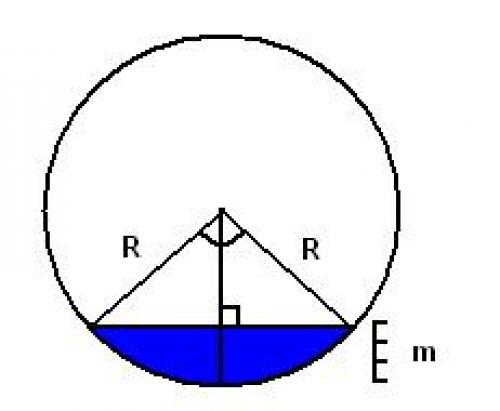
Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.

Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.

Площадь сектора находится как, где альфа — это угол дуги в радианах.

Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,соответственнои ответ нам Javascript даст как раз в радианах, то что нам нужно.

Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен

Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона —.где

Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.